Sets in Python

In Python, a Set is an unordered collection of data items that are unique. In other words, Python Set is a collection of elements (Or objects) that contains no duplicate elements.

Unlike List, Python Set doesn’t maintain the order of elements, i.e., It is an unordered data set. So you cannot access elements by their index or perform insert operation using an index number.

In this tutorial, we will learn Set data structure in general, different ways of creating them, and adding, updating, and removing the Set items. We will also learn the different set operations.

Characteristics of a Set

A set is a built-in data structure in Python with the following three characteristics.

1. Unordered: The items in the set are unordered, unlike lists, i.e., it will not maintain the order in which the items are inserted. The items will be in a different order each time when we access the Set object. There will not be any index value assigned to each item in the set.
2. Unchangeable: Set items must be immutable. We cannot change the set items, i.e., We cannot modify the items’ value. But we can add or remove items to the Set. A set itself may be modified, but the elements contained in the set must be of an immutable type.
3. Unique: There cannot be two items with the same value in the set.

Creating a Set

There are following two ways to create a set in Python.

• Using curly brackets: The easiest and straightforward way of creating a Set is by just enclosing all the data items inside the curly brackets {}. The individual values are comma-separated.
• Using set() constructor: The set object is of type class 'set'. So we can create a set by calling the constructor of class ‘set’. The items we pass while calling are of the type iterable. We can pass items to the set constructor inside double-rounded brackets.

Let’s see each one of them with an example.

# create a set using {}
# set of mixed types intger, string, and floats
sample_set = {'Mark', 'Jessa', 25, 75.25}
print(sample_set)
# Output {25, 'Mark', 75.25, 'Jessa'}

# create a set using set constructor
# set of strings
book_set = set(("Harry Potter", "Angels and Demons", "Atlas Shrugged"))
print(book_set)
# output {'Harry Potter', 'Atlas Shrugged', 'Angels and Demons'}

print(type(book_set))  
# Output class 'set'

Note:

• As we can see in the above example the items in the set can be of any type like String, Integer, Float, or Boolean. This makes a Set Heterogeneous i.e. items of different types can be stored inside a set.
• Also, the output shows all elements are unordered.

Create a set from a list

Also, set eliminating duplicate entries so if you try to create a set with duplicate items it will store an item only once and delete all duplicate items. Let’s create a set from an iterable like a list. We generally use this approach when we wanted to remove duplicate items from a list.

Example

# list with duplicate items
number_list = [20, 30, 20, 30, 50, 30]
# create a set from a list
sample_set = set(number_list)

print(sample_set)
# Output {50, 20, 30}

Creating a set with mutable elements

You will get an error if you try to create a set with mutable elements like lists or dictionaries as its elements.

Example

# set of mutable types
sample_set = {'Mark', 'Jessa', [35, 78, 92]}
print(sample_set)
# Output TypeError: unhashable type: 'list' [35, 78, 92]

Empty set

When we don’t pass any item to the set constructor then it will create an empty set.

empty_set = set()
print(type(empty_set)) 
# class 'set'

When the same object ‘person’ is created without any items inside the curly brackets then it will be created as a dictionary which is another built-in data structure in Python.

So whenever you wanted to create an empty set always use the set() constructor.

emptySet = {}
print(type(emptySet)) # class 'dict'

Accessing items of a set

The items of the set are unordered and they don’t have any index number. In order to access the items of a set, we need to iterate through the set object using a for loop

book_set = {"Harry Potter", "Angels and Demons", "Atlas Shrugged"}
for book in book_set:
    print(book)

Output:

Angels and Demons
Atlas Shrugged
Harry Potter

As we can see in the output, the items’ order is not the same as their insertion order. And each time this order will be changing, there is no index value attached to each item.

Checking if an item exists in Set

As mentioned above the Set is an unordered collection and thereby can’t find items using the index value. In order to check if an item exists in the Set, we can use the in operator.

The in operator checks whether the item is present in the set, and returns True if it present otherwise, it will return False.

book_set = {"Harry Potter", "Angels and Demons", "Atlas Shrugged"}
if 'Harry Potter' in book_set:
    print("Book exists in the book set")
else:
    print("Book doesn't exist in the book set")
# Output Book exists in the book set

# check another item which is not present inside a set
print("A Man called Ove" in book_set)  
# Output False

Here the ‘Harry Potter’ item is present in the bookset and it returns true.

Find the length of a set

To find the length of a Set, we use the len() method. This method requires one parameter to be passed, the set’s name whose size we need to find.

# create a set using set constructor
book_set = {"Harry Potter", "Angels and Demons", "Atlas Shrugged"}
print(len(book_set))
# Output 3

As we can see in the above output the len() method returns an integer 3. This is equal to the number of items present in the Set.

Adding items to a Set

Though the value of the item in a Set can’t be modified. We can add new items to the set using the following two ways.

1. The add() method: The add() method is used to add one item to the set.
2. Using update() Method: The update() method is used to multiple items to the Set. We need to pass the list of items to the update() method

Example

book_set = {'Harry Potter', 'Angels and Demons'}
# add() method
book_set.add('The God of Small Things')
# display the updated set
print(book_set)
# Output {'Harry Potter', 'The God of Small Things', 'Angels and Demons'}

# update() method to add more than one item
book_set.update(['Atlas Shrugged', 'Ulysses'])
# display the updated set
print(book_set)
# Output {'The God of Small Things', 'Angels and Demons', 'Atlas Shrugged', 'Harry Potter', 'Ulysses'}

As we can see we have added a single book to the book set using the add() method and two different books to this bookset in a single statement using the update() method.

Removing item(s) from a set

In order to remove the items from a Set, we can use any one of the following set methods

Method	Description
remove()	To remove a single item from a set. This method will take one parameter, which is the item to be removed from the set. Throws a keyerror if an item not present in the original set
discard()	To remove a single item that may or may not be present in the set. This method also takes one parameter, which is the item to be removed. If that item is present, it will remove it. It will not throw any error if it is not present.
pop()	To remove any random item from a set
clear()	To remove all items from the Set. The output will be an empty set
del set	Delete the entire set

Let’s see an example to delete single or multiple items from a set.

Example

color_set = {'red', 'orange', 'yellow', 'white', 'black'}

# remove single item
color_set.remove('yellow')
print(color_set)
# Output {'red', 'orange', 'white', 'black'}

# remove single item from a set without raising an error
color_set.discard('white')
print(color_set)
# Output {'orange', 'black', 'red'}

# remove any random item from a set
deleted_item = color_set.pop()
print(deleted_item)

# remove all items
color_set.clear()
print(color_set)
# output set()

# delete a set
del color_set

remove() vs discard()

• The remove() method throws a keyerror if the item you want to delete is not present in a set
• The discard() method will not throw any error if the item you want to delete is not present in a set

Example

color_set = {'red', 'orange', 'white', 'black'}

# remove single item using discard()
color_set.discard('yellow')
print(color_set)
# Output {'red', 'black', 'white', 'orange'}

# remove single item using remove()
color_set.remove('yellow')
print(color_set)
# Output KeyError: 'yellow'

Set Operations

All the operations that could be performed in a mathematical set could be done with Python sets. We can perform set operations using the operator or the built-in methods defined in Python for the Set.

The following table will summarize the set operations and the corresponding set method used.

Operation	Definition	Operator	Method
Union	All the items of both Sets will be returned. Only the duplicate items will be dropped.	|	union()
Intersection	Only the items common in both sets will be returned.	&	intersection()
Difference	Return the unique elements in the first set which is not in the second set.	-	difference()
Symmetric Difference	Return the elements of both sets which is not common.	^	symmetric_difference()

Let us see each one of them with an example.

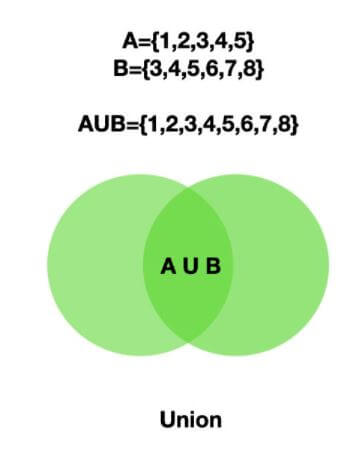
Union of sets

Union of two sets will return all the items present in both sets (all items will be present only once). This can be done with either the | operator or the union() method.

The following image shows the union operation of two sets A and B.

Example

color_set = {'violet', 'indigo', 'blue', 'green', 'yellow'}
remaining_colors = {'indigo', 'orange', 'red'}

# union of two set using OR operator
vibgyor_colors = color_set | remaining_colors
print(vibgyor_colors)
# Output {'indigo', 'blue', 'violet', 'yellow', 'red', 'orange', 'green'}

# union using union() method
vibgyor_colors = color_set.union(remaining_colors)
print(vibgyor_colors)
# Output {'indigo', 'blue', 'violet', 'yellow', 'red', 'orange', 'green'}

Here we can see all the items in both sets are printed and the items that are present in both are printed only once.

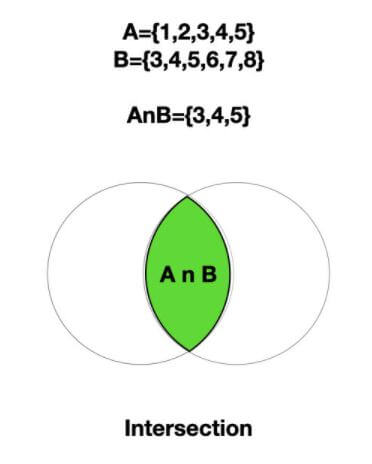
Intersection of Sets

The intersection of two sets will return only the common elements in both sets. The intersection can be done using the & operator and intersection() method.

The intersection() method will return a new set with only the common elements in all the sets. Use this method to find the common elements between two or more sets.

The following image shows the intersection operation of two sets A and B.

Example

color_set = {'violet', 'indigo', 'blue', 'green', 'yellow'}
remaining_colors = {'indigo', 'orange', 'red'}

# intersection of two set using & operator
new_set = color_set & remaining_colors
print(new_set)
# Output {'indigo'}

# using intersection() method
new_set = color_set.intersection(remaining_colors)
print(new_set)
# Output {'indigo'}

Intersection update

In addition to the above intersection() method, we have one more method called intersection_update().

There are two key differences between intersection() and intersection_update()

• intersection() will not update the original set but intersection_update() will update the original set with only the common elements.
• intersection() will have a return value which is the new set with common elements between two or more sets whereas intersection_update() will not have any return value.

Let us see this with a small example.

color_set = {'violet', 'indigo', 'blue', 'green', 'yellow'}
remaining_colors = {'indigo', 'orange', 'red'}

# intersection of two sets
common_colors = color_set.intersection(remaining_colors)
print(common_colors)  # output {'indigo'}
# original set after intersection
print(color_set)
# Output {'indigo', 'violet', 'green', 'yellow', 'blue'}

# intersection of two sets using intersection_update()
color_set.intersection_update(remaining_colors)
# original set after intersection
print(color_set)
# output {'indigo'}

As we can see in the above example the intersection() method is returning a new set with common elements while the intersection_update() is returning ‘None’.

The original set remains the same after executing the  intersection() method, while the original set is updated after the intersection_update().

Difference of Sets

The difference operation will return the items that are present only in the first set i.e the set on which the method is called. This can be done with the help of the - operator or the difference() method.

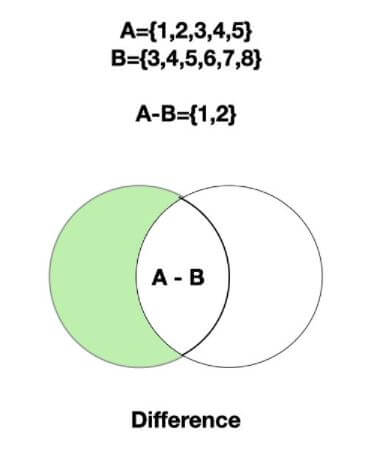
The following image shows the set difference between two sets A and B.
Example

color_set = {'violet', 'indigo', 'blue', 'green', 'yellow'}
remaining_colors = {'indigo', 'orange', 'red'}

# difference using '-' operator
print(color_set - remaining_colors)
# output {'violet', 'blue', 'green', 'yellow'}

# using difference() method
print(color_set.difference(remaining_colors))
# Output {'violet', 'blue', 'green', 'yellow'}

As we can see the first one returns the items that are present only in the first set and the second returns the items that are present in the second set.

Difference update

In addition to the difference(), there is one more method called difference_update(). There are two main differences between these two methods.

• The difference() method will not update the original set while difference_update() will update the original set.
• The difference() method will return a new set with only the unique elements from the set on which this method was called. difference_update() will not return anything.

Example

color_set = {'violet', 'indigo', 'blue', 'green', 'yellow'}
remaining_colors = {'indigo', 'orange', 'red'}

# difference of two sets
new_set = color_set.difference(remaining_colors)
print(new_set)
# output {'violet', 'yellow', 'green', 'blue'}
# original set after difference
print(color_set)
# {'green', 'indigo', 'yellow', 'blue', 'violet'}

# difference of two sets
color_set.difference_update(remaining_colors)
# original set after difference_update
print(color_set)
# Output {'green', 'yellow', 'blue', 'violet'}

This output shows that the original set is not updated after the difference() method i.e, the common element indigo is still present whereas the original set is updated in difference_update() .

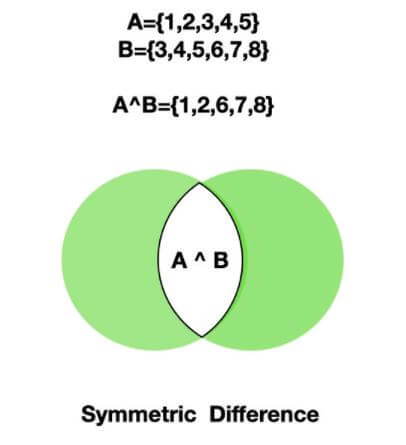
Symmetric difference of Sets

The Symmetric difference operation returns the elements that are unique in both sets. This is the opposite of the intersection. This is performed using the ^ operator or by using the symmetric_difference() method.

The following image shows the symmetric difference between sets A and B.

Example

color_set = {'violet', 'indigo', 'blue', 'green', 'yellow'}
remaining_colors = {'indigo', 'orange', 'red'}

# symmetric difference between using ^ operator
unique_items = color_set ^ remaining_colors
print(unique_items)
# Output {'blue', 'orange', 'violet', 'green', 'yellow', 'red'}

# using symmetric_difference()
unique_items2 = color_set.symmetric_difference(remaining_colors)
print(unique_items2)
# Output {'blue', 'orange', 'violet', 'green', 'yellow', 'red'}

Symmetric difference update

In addition to the symmetric_difference(), there is one more method called symmetric_difference_update(). There are two main differences between these two methods.

The symmetric_difference() method will not update the original set while symmetric_difference_update() will update the original set with the unique elements from both sets.

Example

color_set = {'violet', 'indigo', 'blue', 'green', 'yellow'}
remaining_colors = {'indigo', 'orange', 'red'}

# symmetric difference
unique_items = color_set.symmetric_difference(remaining_colors)
print(unique_items)
# output {'yellow', 'green', 'violet', 'red', 'blue', 'orange'}
# original set after symmetric difference
print(color_set)
# {'yellow', 'green', 'indigo', 'blue', 'violet'}

# using symmetric_difference_update()
color_set.symmetric_difference_update(remaining_colors)
# original set after symmetric_difference_update()
print(color_set)
# {'yellow', 'green', 'red', 'blue', 'orange', 'violet'}

This output shows that the original set is not updated after the symmetric_difference() method  with the same set of elements before and after the operation whereas the original set is updated in symmetric_difference_update() and the return value is None in the case of the symmetric_difference_update().

Copying a Set

In Python, we can copy the items from one set to another in three ways.

• Using copy() method.
• Using the set() constructor
• Using the = (assignment) operator (assigning one set to another)

The difference is while using the=  (assignment) operator any modifications we make in the original set will be reflected in the new set. But while using the copy() method, the new set will not reflect the original set’s changes.

When you set set2= set11, you are making them refer to the same dict object, so when you modify one of them, all references associated with that object reflect the current state of the object. So don’t use the assignment operator to copy the set instead use the copy() method or set() constructor.

Let us see this with an example.

color_set = {'violet', 'blue', 'green', 'yellow'}

# creating a copy using copy()
color_set2 = color_set.copy()

# creating a copy using set()
color_set3 = set(color_set)

# creating a copy using = operator
color_set4 = color_set

# printing the original and new copies
print('Original set:', color_set)
# {'violet', 'green', 'yellow', 'blue'}

print('Copy using copy():', color_set2)
# {'green', 'yellow', 'blue', 'violet'}

print('Copy using set(): ', color_set3)
# {'green', 'yellow', 'blue', 'violet'}

print('Copy using assignment', color_set4)
# {'green', 'yellow', 'blue', 'violet'}

Here in the above output, the item ‘indigo’ is added to the color_set after copying the contents to color_set2 , color_set3, and color_set4.

We can see that the modification we did in the original set after copying is reflected in the color_set4 created with the = operator.

Subset and Superset

In Python, we can find whether a set is a subset or superset of another set. We need to use the set methods issubset() and issuperset.

issubset()

The issubset() is used to find whether a set is a subset of another set i.e all the items in the set on which this method is called are present in the set which is passed as an argument.

This method will return true if a set is a subset of another set otherwise, it will return false.

issuperset()

This method determines whether the set is a superset of another set.

It checks whether the set on which the method is called contains all the items present in the set passed as the argument and returns true if the set is a superset of another set; otherwise, it will return false.

Example:

color_set1 = {'violet', 'indigo', 'blue', 'green', 'yellow', 'orange', 'red'}
color_set2 = {'indigo', 'orange', 'red'}

# subset
print(color_set2.issubset(color_set1))
# True
print(color_set1.issubset(color_set2))
# False

# superset
print(color_set2.issuperset(color_set1))
# False
print(color_set1.issuperset(color_set2))
# True

find whether two sets are disjoint

The isdisjoint() method will find whether two sets are disjoint i.e there are no common elements. This method will return true if they are disjoint otherwise it will return false.

Example

color_set1 = {'violet', 'blue', 'yellow', 'red'}
color_set2 = {'orange', 'red'}
color_set3 = {'green', 'orange'}

# disjoint
print(color_set2.isdisjoint(color_set1))
# Output 'False' because contains 'red' as a common item

print(color_set3.isdisjoint(color_set1))
# Output 'True' because no common items

Sort the set

A set is an unordered collection of data items, so there is no point n sorting it. If you still want to sort it using the sorted() method but this method will return the list

The sorted() function is used to sort the set. This will return a new list and will not update the original set.

Example

set1 = {20, 4, 6, 10, 8, 15}
sorted_list = sorted(set1)
sorted_set = set(sorted_list)
print(sorted_set)
# output {4, 6, 8, 10, 15, 20}

Using Python built-in functions for Set

In addition to the built-in methods that are specifically available for Set, there are few common Python Built-In functions. Let us see how we can use a few of them for sets with examples.

all() and any()

• The built-in function all() returns true only when all the Set items are True. If there is one Zero in the case of integer set or one False value then it will return false.
• Thie built-in function any() returns true if any item of a set is True. This will return false when all the items are False.

Let us see an example with a different combination of values inside a set.

set1 = {1, 2, 3, 4}
set2 = {0, 2, 4, 6, 8}  # set with one false value '0'
set3 = {True, True}  # set with all true
set4 = {True, False}  # set with one false
set5 = {False, 0}  # set with both false values

# checking all true value set
print('all() With all true values:', all(set1))  # True
print('any() with all true Values:', any(set1))  # True

# checking one false value set
print('all() with one Zero:', all(set2))  # False
print('any() with one Zero:', any(set2))  # True

# checking with all true boolean
print('all() with all True values:', all(set3))  # True
print('any() with all True values:', any(set3))  # True

# checking with one false boolean
print('all() with one False value:', all(set4))  # False
print('any() with one False:', any(set4))  # True

# checking with all false values
print('all() with all False values:', all(set5))  # False
print('any() with all False values:', any(set5))  # False

max() and min()

The max() function will return the item with maximum value in a set. Similarly, min() will return an item with a minimum value in a set.

In the case of a set with strings, it will compute the maximum/minimum value based on the ASCII Code.

Example

set1 = {2, 4, 6, 10, 8, 15}
set2 = {'ABC', 'abc'}

# Max item from integer Set
print(max(set1))  # 15

# Max item from string Set
print(max(set2))  # abc

# Minimum item from integer Set
print(min(set1))  # 2

# Minimum item from string Set
print(min(set2))  # ABC

Frozen Set

A frozenset  is an immutable set. Frozen Set is thus an unordered collection of immutable unique items.

We can create a frozenset using the frozenset() function, which takes a single iterable object as a parameter.

Example

rainbow = ('violet', 'indigo', 'blue', 'green', 'yellow', 'orange', 'red')
# create a frozenset
f_set = frozenset(rainbow)

print(f_set)
# output frozenset({'green', 'yellow', 'indigo', 'red', 'blue', 'violet', 'orange'})

As seen in the above example the colors of the rainbow are created as a frozenset inside a {} brackets. If we don’t pass any item then it will return an empty frozenset.

When to use frozenset ?

• When you want to create an immutable set that doesn’t allow adding or removing items from a set.
• When you want to create a read-only set

Now if we try to drop or add any item then it will throw an error as a frozen set is immutable.

rainbow = ('violet', 'indigo', 'blue')
f_set = frozenset(rainbow)
# Add to frozenset
f_set.add(f_set)
# output AttributeError: 'frozenset' object has no attribute 'add'

All the mathematical operations performed in a set is possible with the frozenset. We can use union(), intersection(), difference(), and symmetric_difference() on a frozenset as well.

But we can’t use the intersection_update(), difference_update(), and symmetric_difference_update() on frozenset as it is immutable.

Example

colorset1 = frozenset(('violet', 'indigo', 'blue', 'green'))
colorset2 = frozenset(('blue', 'green', 'red'))

# Mathametical operations with a frozen set

# union
print('The colors of the rainbow are:', colorset1.union(colorset2))
# output frozenset({'red', 'green', 'blue', 'violet', 'indigo'})

# intersection
print('The common colors are:', colorset1.intersection(colorset2))
# output frozenset({'green', 'blue'})

# difference
print('The unique colors in first set are:', colorset1.difference(colorset2))
# output frozenset({'violet', 'indigo'})

print('The unique colors in second set are:', colorset2.difference(colorset1))
# output frozenset({'red'})

# symmetric difference
print('The unique colors second set are:', colorset1.symmetric_difference(colorset2))
# output frozenset({'indigo', 'red', 'violet'})

Nested Sets

As we understand the value of the elements in the set cannot be changed. A set cannot have mutable objects as its elements. So we can’t have another set inside a set.

In case we try to add another set as an element to a set then we get the 'Type Error: unhashable type: 'set' '. This is because a set is not hashable. (A Hashable object is one whose value will not change during its lifetime).

To create a nested Set we can add a frozenset as an item of the outer set. The frozenset is again a set but it is immutable.

Let us see this with an example.

rainbow = ('violet', 'indigo', 'blue', 'green', 'yellow', 'orange', 'red')
other_colors = ('white', 'black', 'pink')

nested_set = set((frozenset(rainbow), frozenset(other_colors)))

for sample_set in nested_set:
    print(sample_set)

Output:

frozenset({'black', 'white', 'pink'})
frozenset({'green', 'violet', 'indigo', 'red', 'blue', 'orange', 'yellow'})

As we can see in the above example we are adding the two frozensets rainbow and othercolors to the colorset. Here the two frozensets are nested inside the outer colorset.

Set comprehension

Set comprehension is one way of creating a Set with iterables generated in a for loop and also provides options to add only the items that satisfy a particular condition. The general syntax is as follows

outputSet = {expression(variable) for variable in inputSet [if variable condition1][if variable condition2]..}

• expression: Optional. expression to compute the members of the output set which satisfies the above conditions
• variable: Required. a variable that represents the members of the input set
• inputSet: Required. Represents the input set
• condition1: Optional. Filter conditions for the members of the output set.

With this Set comprehension, we can reduce a lot of code while creating a Set.

Let’s see the example of creating a set using set comprehension, which will have the square of all even numbers between the range 1 to 10.
In the above example, first, we are computing a set with the square of even numbers from the input set.

# creating a set with square values of the even numbers
square_set = {var ** 2 for var in range(1, 10) if var % 2 == 0}
print(square_set)
# Output {16, 64, 4, 36}

When to use a Set Data structure?

It is recommended to use a set data structure when there are any one of the following requirements.

• Eliminating duplicate entries: In case a set is initialized with multiple entries of the same value, then the duplicate entries will be dropped in the actual set. A set will store an item only once.
• Membership Testing: In case we need to check whether an item is present in our dataset or not, then a Set could be used as a container. Since a Set is implemented using Hashtable, it is swift to perform a lookup operation, i.e., for each item, one unique hash value will be calculated, and it will be stored like a key-value pair.
  So to search an item, we just have to compute that hash value and search the table for that key. So the speed of lookup is just O(1).
• Performing arithmetic operations similar to Mathematical Sets: All the arithmetic operations like union, Intersection, finding the difference that we perform on the elements of two sets could be performed on this data structure.